La teoria dei Polimini

I polimini di Solomon W. Golomb

Un semplice foglio a quadretti è il punto di partenza per scoprire un universo di figure davvero ricco dalle quali si possono ricavare molti giochi divertenti e numerosi rompicapo. Un foglio come quello che aveva davanti a sé Solomon Wolf Golomb, nel 1953 quando, giovane studente statunitense di Harvard, per superare la noia di una lezione poco interessante per lui, incominciò a tracciare una serie di figure che avevano il quadretto come punto di partenza.

Da bravo matematico, tentò poi di classificarle, cercando di stabilire quante figure diverse fosse possibile costruire con un quadretto, con due, tre, quattro quadretti e così via, stabilendo però una regola precisa: i quadretti che componevano le varie figure dovevano avere almeno un lato in comune e si dovevano considerare equivalenti tutte quelle che potevano essere sovrapposte con un movimento qualsiasi.

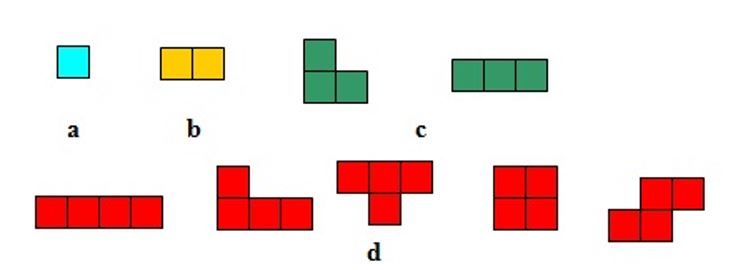
Golomb chiamò polimini le figure così ottenute. In particolare, battezzò monomino il quadretto base. duomino (domino) l’unica figura che si puà costruire con due quadretti, trimini quelle formate da tre quadretti, tetramini quelle di quattro quadretti, pentamini di cinque e così via, sempre tenendo presente la regola che i quadretti devono avere almeno un lato in comune e che si devono escludere le figure equivalenti.

Polimini e matematica ricreativa

La matematica ricreativa riguarda attività che sono praticate con un preciso fine di divertimento personale e che sono rivolte ad oggetti con contenuti matematici di rilievo, anche se spesso non esplicitato. Essa si occupa primariamente di giochi matematici di tanti tipi, ma estende i propri interessi anche a questioni come le soluzioni di rompicapo che richiedono ragionamenti deduttivi e ad aree come la logica matematica e la pedagogia della matematica. Alcuni dei più interessanti problemi di questo campo non richiedono conoscenze della matematica avanzata.

Questo argomento può toccare anche problemi come l’estetica della matematica, occuparsi di storie divertenti, curiose o peculiari di oggetti e persone della matematica. La matematica ricreativa comprende l’osservazione di configurazioni matematiche come i quadrati magici e i frattali, questi ultimi con l’aiuto di strumenti di computer grafica.

Le maggiori potenzialità della matematica ricreativa consistono nello stimolare certe abilità matematiche, nell’avvicinare in modo piacevole allo studio della matematica facendo superare la fama della matematica come conoscenza pedante e accessibile a pochi.

Se vuoi qualche esempio di laboratori di Matematica ricreativa clicca QUI.

Come molti rompicapi della matematica ricreativa, i polimini sono interessanti dal punto di vista combinatorio. Lo studio dei polimini consiste infatti nello stabilire il numero di differenti tipi che si possono ottenere in funzione del numero n di celle formate dal quadrato di base e delle regole di costruzione. Purtroppo non esiste una formula generale per farlo, anche se esistono diversi algoritmi che permettono una stima affidabile. In generale si è stimato che il numero di n-polimini cresce esponenzialmente all’aumentare di n. Esistono anche diversi polimini con buchi, che di solito sono però ignorati perché si considerano solo quelli semplicemente connessi.

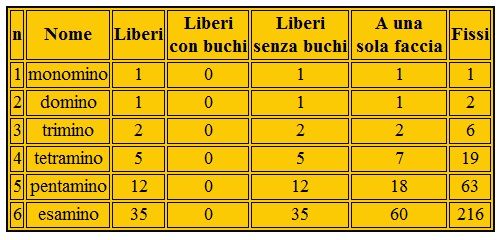
Esistono tre diversi modi di distinguere i polimini:

– I polimini liberipolimini liberipolimini liberipolimini liberi sono quelli che non derivano da alcuna trasformazione rigida (traslazione, rotazione, riflessione o antitraslazione) di altri polimini (si tratta di figure che possono essere sollevate e capovolte).

– I polimini a una sola faccia sono quelli che non derivano da traslazione o rotazione di un altro polimino.

– I polimini fissi, infine, sono quelli che non derivano da una traslazione di un altro polimino (sono figure che non possono essere capovolte o ruotate). La tabella elenca i diversi polimini con n celle fino a 6:

Egli presentò all’Harvard Mathematics Club il suo gioco, che divenne ben presto molto popolare fra gli studenti.

Fu poi Martin Gardner, il massimo esperto in giochi matematici, a rilanciarlo in tutto il mondo attraverso le sue pagine di Scientific American.

Solomon Wolf Golomb è noto per essere l’inventore dei polimini e di una variante della dama nota come Cheskers. Era specialista in problemi di calcolo combinatorio, teoria dei numeri, teoria dei codici e le comunicazioni. Il notissimo gioco Tetris (creato nel 1984 nell’ex unione Sovietica da Alexy Pajitnov) ha tratto ispirazione dai suoi tetramini, dove le diverse forme cadono una alla volta mentre il giocatore deve ruotarli e/o muoverli in modo che creino una riga orizzontale di blocchi senza interruzioni. Quando la riga è stata creata, i mattoni spariscono e i pezzi sovrastanti (se ce ne sono) cadono a formare nuove linee. Poiché nel gioco è ammessa solo la rotazione dei pezzi e non il ribaltamento, ai cinque tetramini liberi sono aggiunti i simmetrici di quelli a forma di L e di Z , in modo da poter disporre di tutte le configurazioni che si possono ottenere componendo simmetrie su un tetramino.

Come lo proponiamo alla scuola primaria?

Come un gioco, una sfida alla quale parteciparecon entusiasmo. “Secondo voi quante figure si possono formare con un quadretto? Con due, a patto che abbiano un lato in comune? Con tre?”

Con i pentamini, in particolare, oltre alle naturali e semplici riflessioni su aree e perimetri (ad esempio, se l’area è costante, come cambiano i perimetri?), si possono svolgere con i bambini più piccoli (anche a partire dalla classe seconda) giochi molto divertenti.

Un classico gioco è quello dei rettangoli: si consegnano ai bambini i 12 pentamini ritagliati e si chiede loro di completare uno a scelta tra questi rettangoli:

– un rettangolo 6×10

– un rettangolo 5×12

– un rettangolo 4×15

– un rettangolo 3×20

(anche qui è utilissima una riflessione su aree e perimetri di queste speciali figure).

Esistono in commercio diversi giochi ispirati ai polimini e sono in assoluto tra i giochi più adatti da portare in classe!!!

Il Polyminix oppure i kit di Learning Resources o, ancora, i tetramini POP-IT e poi il gioco da tavolo Level 9 sono solo alcuni esempi dei materiali disponibili online.

Molti sono i siti che riportano notizie sui polimini; per approfondire il tema e trovare una sitografia specifica, si suggerisce quello relativo al Progetto Polymath del Politecnico di Torino. Altri siti raccolgono vari giochi con i polimini: a livello di scuola primaria parecchie proposte utilizzano il software di geometria dinamica Geo Gebra per ricostruire con i pentamini diverse figure (un esempio: http://splashragazzi.altervista.org/pentamini-con-geogebra).

Tanti interessanti giochi per PC e materiali in PDF li ho trovati qui: https://www.tiziana1.it/polimini.htm e qui: https://emmametodo.com ma per comodità ho pensato di fare una raccolta dei materiali utili su Freeed in modo da salvarlo nelle raccolte ed averli sempre a portata di “cellulare”!

Inoltre sono presenti sul web le esperienze di tanti insegnanti e video utilissimi su Youtube.